티스토리 뷰
이 카테고리에서는 단순히 수학적 공식 혹은 지식을 깊게 다루진 않는다.
프로그래밍과 연관 지어서 유용하게 사용할 수 있는 수학적 지식을 다룬다.
| Honor's Method
호너의 방법, 호너 메서드, 호너의 법칙 이라고도 하는 Honor's Method는 영국의 수학자인 윌리엄 조지 호너의 이름을 따서 지어진 다항식을 표현하는 방법이다.
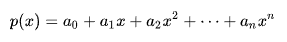
위와 같은 다항식이 있을 때 이를 Honor's Method로 표현하면 아래와 같다.

Honor's Method로 표현한 위의 다항식을 살펴보면 단순히 x로 묶은 것 그 이상 그 이하도 아니다. 하지만 이를 프로그래밍에서 활용하면 계산량을 많이 줄일 수 있다.
예를 들어 아래와 같은 다항식이 있다고 하자.
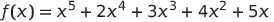
이를 단순하게 프로그래밍 한다면 x의 n승을 구하는데 5 + 4 + 3 + 2 +1으로 총 15번 + 계수를 곱하는데 5번 해서 20번의 곱셈이 필요하다. 하지만 함수를 아래와 같이 묶어준다면 ?
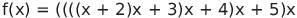
이렇게 표현이 가능하고 단순히 덧셈과 4번 곱셈 4번이 반복되는 계산으로 바꿔줄 수 있다.
즉, 다항식을 코드로 표현하면 아래와 같은 방법으로 간단하게 표현이 가능하다.
int honor_method(int x) {
size_t arr[5] = {1, 2, 3, 4, 5};
int result = arr[0];
for(int i=1; i<5; ++i) {
result = (result * x) + arr[i];
}
return result;
}추가적으로 Honor's Method는 다른 방면에서도 활용되는 몇 가지 예를 추가한다.
1. 진법 변환
만약 어떠한 A진법으로 표현된 숫자를 B진법으로 변환한다고 가정하자. 일반적으로 생각할 수 있는 방법은, A진법으로 표현된 수를 10진법으로 바꾸고 이를 다시 B진법으로 변환하는 방법이다. 여기서 10진법으로 바꾸는 과정에 Honor Method's를 사용 가능하다.
// A진법의 어떠한 수가 문자열 S로 주어짐.
for(int i=0; S[i]; ++i) {
if(s[i] < 'A') {
d = d * A + S[i] - '0'; // 10진법 보다 작은 진법일 때
} else {
d = d * A + S[i] - 'A' + 10; // 10진법 보다 큰 진법일 때
}
}
// 작성중..
'IT > Math' 카테고리의 다른 글
| [수학과 프로그래밍] 2의 승수의 합 (등비수열의 합) (0) | 2022.08.17 |
|---|---|
| [수학과 프로그래밍] 1부터 N까지의 합 (0) | 2022.08.15 |
| [수학과 프로그래밍] 소수점을 이진수로 (0) | 2022.07.14 |
- Total
- Today
- Yesterday
- rust
- 내돈내산
- 러스트 기초
- 속초
- 기술면접
- 러스트 입문
- 트리
- 반드시 알아야 할 자료구조
- 속초 맛집
- 자료구조
- Tree
- interview question
- LeetCode
- C++
- algorithm
- DP
- 인터뷰
- 코딩인터뷰
- 솔직후기
- 러스트 배우기
- Problem Solving
- 러스트
- Medium
- coding interview
- PS
- 맛집
- ProblemSolving
- 리트코드
- 알고리즘
- Interview
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
